高起点数学（文）复习要点（二）

数学（文）复习要点

一、正比例函数

解析式：y＝kx。

图像是过原点的直线。

①当k＞0时，y随x的增大而增大，此时图像是过第一、第三象限及原点的直线；

②当k＜0时，y随x的增大而减小，此时图像是过第二、第四象限及原点的直线。

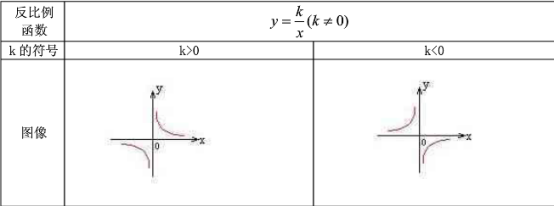
二、反比例函数

解析式：y＝k/x。

图像是以坐标轴为渐近线的双曲线。

①当k＞0时，y随x的增大而减小，此时图像在第一、第三象限；

②当k＜0时，y随x的增大而增大，此时图像在第二、第四象限。

三、一次函数

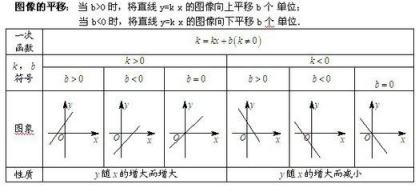
解析式：y＝kx＋b

①当b＝0时，为正比例函数，其图像与性质见前面所述；

②当k＞0，且b＞0时，y随x的增大而增大，此时图像是与x轴负半轴、y轴正半轴相交的直线；

③当k＞0，且b＜0时，y随x的增大而增大，此时图像是与x轴正半轴、y轴负半轴相交的直线；

④当k＜0，且b＞0时，y随x的增大而减小，此时图像是与x轴正半轴、y轴正半轴相交的直线；

⑤当k＜0，且b＜0时，y随x的增大而减小，此时图像是与x轴负半轴、y轴负半轴相交的直线。

二次函数

I.定义与定义表达式

一般地，自变量x和因变量y之间存在如下关系：

y=ax2+bx+c（a，b，c为常数，a≠0，且a决定函数的开口方向，a>0时，开口方向向上，a<0时，开口方向向下, |a|还可以决定开口大小, |a|越大开口就越小, |a|越小开口就越大.）

则称y为x的二次函数。

二次函数表达式的右边通常为二次三项式。

II.二次函数的三种表达式

一般式：y=ax2;+bx+c（a，b，c为常数，a≠0）

顶点式：y=a(x-h) 2;+k [抛物线的顶点P（h，k）]

交点式：y=a(x-x1)(x-x2) [仅限于与x轴有交点A（x1，0）和 B（x2，0）的抛物线]

注：在3种形式的互相转化中，有如下关系:

h=-b/2a ,k=(4ac-b2)/4a ,x1,x2=(-b±√b2;-4ac)/2a

III.二次函数的图像

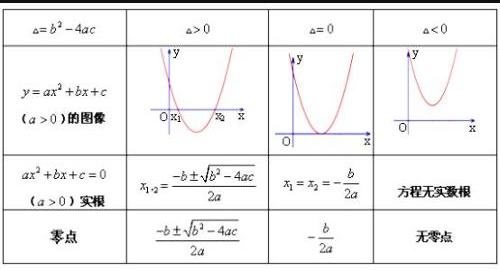
三个“二次”及关系

三个“二次”即一元二次函数、一元二次方程、一元二次不等式是中学数学的重要内容，具有丰富的内涵和密切的联系，同时也是研究包含二次曲线在内的许多内容的工具.高考试题中近一半的试题与这三个“二次”问题有关.本节主要是帮助考生理解三者之间的区别及联系，掌握函数、方程及不等式的思想和方法.

●难点

已知对于x的所有实数值，二次函数f(x)=x2-4ax+2a+12(a∈R)的值都是非负的，求关于x的方程 =|a-1|+2的根的取值范围.

●案例

[例1]已知二次函数f(x)=ax2+bx+c和一次函数g(x)=-bx，其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R).

(1)求证：两函数的图象交于不同的两点A、B;

(2)求线段AB在x轴上的射影A1B1的长的取值范围.

命题意图：本题主要考查考生对函数中函数与方程思想的运用能力.属于★★★★★题目.

知识依托：解答本题的闪光点是熟练应用方程的知识来解决问题及数与形的完美结合.

错解分析：由于此题表面上重在“形”，因而本题难点就是一些考生可能走入误区，老是想在“形”上找解问题的突破口，而忽略了“数”.

技巧与方法：利用方程思想巧妙转化.

证明：由 消去y得ax2+2bx+c=0

Δ=4b2-4ac=4(-a-c)2-4ac=4(a2+ac+c2)=4[(a+ c2]

∵a+b+c=0,a>b>c,∴a>0,c<0

∴ c2>0,∴Δ>0,即两函数的图象交于不同的两点.

本文章来源于网络，如有侵权，请联系本网站