 您现在位置:首页> 备考辅导>
成考高起专>
数学(理)>
浏览文章
您现在位置:首页> 备考辅导>
成考高起专>
数学(理)>
浏览文章
数学(理)复习要点
一、正比例函数
解析式:y=kx。
图像是过原点的直线。
①当k>0时,y随x的增大而增大,此时图像是过第一、第三象限及原点的直线;
②当k<0时,y随x的增大而减小,此时图像是过第二、第四象限及原点的直线。

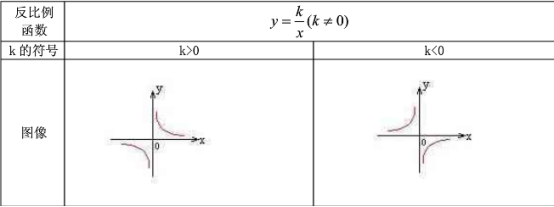
二、反比例函数
解析式:y=k/x。
图像是以坐标轴为渐近线的双曲线。
①当k>0时,y随x的增大而减小,此时图像在第一、第三象限;
②当k<0时,y随x的增大而增大,此时图像在第二、第四象限。
三、一次函数
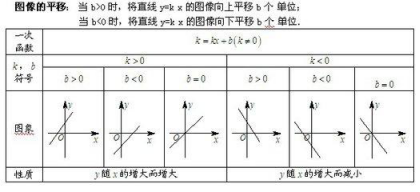
解析式:y=kx+b
①当b=0时,为正比例函数,其图像与性质见前面所述;
②当k>0,且b>0时,y随x的增大而增大,此时图像是与x轴负半轴、y轴正半轴相交的直线;
③当k>0,且b<0时,y随x的增大而增大,此时图像是与x轴正半轴、y轴负半轴相交的直线;
④当k<0,且b>0时,y随x的增大而减小,此时图像是与x轴正半轴、y轴正半轴相交的直线;
⑤当k<0,且b<0时,y随x的增大而减小,此时图像是与x轴负半轴、y轴负半轴相交的直线。
夏天:
二次函数
I.定义与定义表达式
一般地,自变量x和因变量y之间存在如下关系:
y=ax2+bx+c(a,b,c为常数,a≠0,且a决定函数的开口方向,a>0时,开口方向向上,a<0时,开口方向向下, |a|还可以决定开口大小, |a|越大开口就越小, |a|越小开口就越大.)
则称y为x的二次函数。
二次函数表达式的右边通常为二次三项式。
II.二次函数的三种表达式
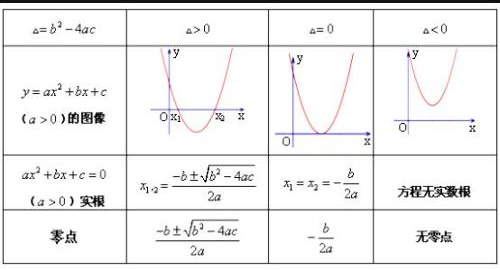
一般式:y=ax2;+bx+c(a,b,c为常数,a≠0)
顶点式:y=a(x-h) 2;+k [抛物线的顶点P(h,k)]
交点式:y=a(x-x1)(x-x2) [仅限于与x轴有交点A(x1,0)和 B(x2,0)的抛物线]
注:在3种形式的互相转化中,有如下关系:
h=-b/2a ,k=(4ac-b2)/4a ,x1,x2=(-b±√b2;-4ac)/2a
III.二次函数的图像
本文章来源于网络,如有侵权,请联系本网站